From<Elixir>, Into<Rust>

I loved learning the Elixir language and how its pragmatic supervision trees and process model taught me the value fault tolerance as a quality of code than of infrastructure. Having safety and failure recovery as an idiomatic culture and mindset of the language made me a better thinker and developer. As a personal preference then in selecting new languages to learn, I look for potentially new perspectives and insights that it ascribes to its pilgrims. In general, a good learning curve is a good indicator since it has much to teach.

Another language to learn that I believe is worth learning is Rust, a system programming language with a strong culture of memory safety. Its pervasive model of ownership and lifetimes alongside its demanding yet helpful compiler makes compiling code both a challenge and thrill. Aside from the higher learning curve, the absence of a garbage collector and virtual machine while proclaiming safety and performance in the face of concurrency is boldly insane. If I do invest, I expect to be more acute about memory issues and be more confident with algorithms.

After reading the main online book, the best way to understand a language for me is by writing code with a project. Since Rust is a safe alternative to the C language, I want to revisit the data structures and algorithms that I avoided because of tricky pointer management. In starting with linked lists, I stumbled across Too Many Linked List online book which was godsend. Reading it next, I want to step it up and implement a tricky data structure that had interesting mechanics to prove my understanding: AVL Trees.

To understand my intent to go back to the basics, I scoffed at C for being too unsafe relative to Java's automatic memory management during my teenage years. What foolish thoughts. Nonetheless, it pushed me away from learning lower level algorithms which I thought of a hole in my knowledge for years. With this regret, I ran cargo new --lib avl_tree_set_rs.

After three weeks of struggling and tangents, I successfully wrote it with green tests. I found my trial a rigorous yet enlightening learning experience. Despite all the resistance and confusion from the compiler, I trust that as long as it compiles, my code and more importantly I feel safe, a similar feeling in Haskell. In this article, indulge me in my experience of implementing a self-balancing binary tree in Rust as a learning project. Hopefully, this is worth your time, helpful or entertaining. So what does it take to implement an AVL Tree in Rust?

(Source code for this article can be found here.)

REQUIREMENT:: This article assumes a rustc version of at least 1.38 for the non-lexical lifetimes if you want to compile or follow the code.

CAVEAT: This is not a tutorial on Rust. I assume you have read the book yourself and somewhat familiar with binary trees or sets. Although my writing may not be technically precise, I want to focus on discussing Rust from a newcomer's perspective. I do my best to link relevant sections from the book to help me explain syntax and concepts, so do visit them if you need to refresh yourself. You can also try running rustup doc --std that opens a local copy of the standard documentation. I found it quite helpful and convenient in understanding functions and methods. If I make any incriminating errors in terminology or code, do file an issue in the article's repository, so we can rectify it and my thanks.

• Corrections

UPDATE 2019-12-18: Credits to jbj for filing a PR in rewriting take and insert without using unsafe by using recursion.

AVL Trees

As a short discussion, ordered binary trees are good at searching values. As more values expand the tree, it becomes less efficient proportional to its height. Thus, rearranging nodes that minimize height maintains lookup efficiency.

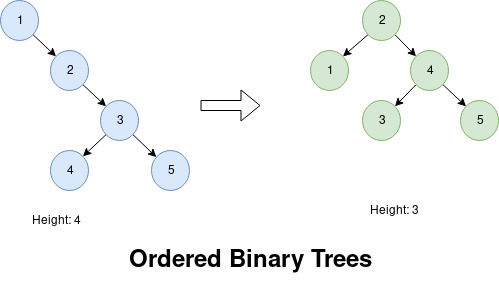
To answer that issue, self-balancing trees balance themselves after every node insertion and deletion. Different variants such Black-Red Trees, Splay Trees and B-Trees are available each with their own strategy. I choose AVL trees for its conceptually simple left and right rotations as its balancing strategy while proving a challenge in Rust because of the pointers that dance in those rotations.

Implementing recursive data structures like trees and graphs in Rust are not trivial because of its ownership model and potential circular references. Specially in insertion and deletion, swapping nodes and values safely and correctly while obeying the rules is tricky itself. Aside from those and some mangling of lifetime variables, we have a modern C language with familiar functional programming concepts at our disposal . Despite the uncertainty, tackling this classic structure with modern ideas makes it feel approachable.

For this project, we will build our AVL tree as a set. To understand idiomatic language design, we will follow and implement methods from the ordered tree set of the standard collection: std::collections::BTreeSet. As much as I would implement every relevant method, the focus of this article is inserting and deleting values from our set that we will discuss in three major sections: insertion, balancing and deletion.

Since this article is long, feel free to stop and come back anytime. Below are links to major sections each with their own links to their subsections:

• Insertion
• Rebalancing
• Deletion
• Beyond Parity (Optional)
• Reflecting On Rust

Insertion

To begin our journey, we will implement the insertion (.insert) method to populate our set and test the values with an iterator (.iter) method. Since implementing balancing strategy is challenging upfront, we will implement it after this to have a working feedback cycle and momentum.

• Data Types
• Insert Method
• Iterator
• Testing Insert

Data Types

What is the design of our tree structure? With some hint from this chapter, we will use a recursive tree design:

#[derive(Debug, PartialEq, Clone)]
struct AvlNode<T: Ord> {
    value: T,
    left: AvlTree<T>,
    right: AvlTree<T>,
}

type AvlTree<T> = Option<Box<AvlNode<T>>>; // What is Box?

#[derive(Debug, PartialEq, Clone)]
struct AvlTreeSet<T: Ord> {
    root: AvlTree<T>,
}

impl<T: Ord> AvlTreeSet<T> {
    fn new() -> Self {
        Self { root: None }
    }
}

To explain some Rust specific details, our set library must take any value that can be ordered, so we declare a generic type that implements the ordering (std::cmp::Ord) trait (T: Ord). The main struct AvlNode expresses a binary tree node that stores a value and possibly has a left and right subtree where the child value is less than and greater than respectively this node's stored value. The newtype/type alias AvlTree represents either an empty value/tree or a node which completes the recursive definition by using the std::option::Option type. Finally, AvlTreeSet provides the interface over the underlying data structure. Optionally, we also derive some useful traits such as debugging via dbg! (std::fmt::Debug), allow equality checks == (std::cmp::PartialEq) and cloning capabilities for testing with .clone (std::clone::Clone).

This design is similar in other languages like Haskell and Java, so we have not strayed far from the path. The snippet below shows how to initialize this:

let mut tree = Some(Box::new(AvlNode {
    value: 2,
    left: Some(Box::new(AvlNode {
        value: 1,
        left: None,
        right: None,
    })),
    right: Some(Box::new(AvlNode {
        value: 5,
        left: Some(Box::new(AvlNode {
            value: 3,
            left: None,
            right: Some(Box::new(AvlNode {
                value: 4,
                left: None,
                right: None,
            })),
        })),
        right: None,
    })),
});

As cumbersome it is to initialize, we encounter our first memory design consideration for recursive structures: std::boxed::Box. Generally, structs or data types should have a known or constant size for memory allocation. Every primitive type has a fixed size such as 1 byte for bool and u8 and 4 bytes for i32 or char. While complex structures can be thought of as a sum of its parts, the compiler cannot infer the known size for recursive structure at compile time since the size is proportional to the level of nesting required at runtime. To resolve this constant and dynamic memory conundrum, since references and pointers also have the same and fixed size, we wrap the recursive data with a heap allocated pointer which stores and points to the data in the heap that satisfies the size constraint and why we wrap each child node with Box::new.

This is unlike other languages where you could use the types without such consideration. Initially awkward, I find it fascinating that Rust requires some forethought to also think about how data is stored (Stack or Heap) at a safe and high level. That this enforced compiler discipline gives me the impression that code in this language is more likely to be planned and deliberate. Definitions done, we proceed with the main method.

Insert Method

Parity: BTreeSet::insert

To insert new values our tree set, we follow a standard procedure for binary trees:

1. Starting from the root node or with a current node
2. Move to the left node if the value is less than the current node, right if greater, and stop if equal
3. Do this until you an empty node and insert the value

Translating this into Rust:

use std::cmp::Ordering;

impl<T: Ord> AvlTreeSet<T> {
    fn insert(&mut self, value: T) -> bool {
        let mut current_tree = &mut self.root;

        // 1. Starting from the root node or with a current node
        while let Some(current_node) = current_tree {
            // 2. Move to the left node if the value is less than the current node,
            //    right if greater, and stop if equal
            match current_node.value.cmp(&value) {
                Ordering::Less => current_tree = &mut current_node.right,
                Ordering::Equal => {
                    return false;
                }
                Ordering::Greater => current_tree = &mut current_node.left,
            }
        }

        // 3. Do this until you an empty node and insert the value
        *current_tree = Some(Box::new(AvlNode {
            value,
            left: None,
            right: None,
        }));

        true
    }
}

With pattern matching, it is easily done and also handles the empty tree case. The snippet below shows how to use it:

let mut set = AvlTreeSet::new();

assert!(set.insert(1));   // Insert new value
assert!(!set.insert(1));  // Should not insert existing value

assert!(set.insert(2));   // Insert another new value
assert_eq!(               // Checking the tree structure
    set.root,
    Some(Box::new(AvlNode {
        value: 1,
        left: None,
        right: Some(Box::new(AvlNode {
            value: 2,
            left: None,
            right: None
        })),
    }))
);

How do we test .insert? We could implement BTreeSet::contains to test if the inserted value is present; however, where it is inserted also matters. If the node is inserted in the left instead of the right, the order of the set would be incorrect. So we need to test it structurally, and we can do that with an tree iterator which we will implement next.

Iterator

Parity: BTreeSet::iter

For our ordered set, we want the iterator to process the data in ascending order, so we will use an in-order traversal or left-node-right approach. Since this is lower level language, we are using a loop instead of a recursive function to express the algorithm:

1. Starting from the root node or with a current node
2. If the node has a left subtree, store this node in a stack of unemitted nodes, then move to the left node and repeat this step
3. Otherwise, emit the value
4. Next if the node has a right subtree, then move to the right node and repeat from step 2
5. If neither and there is an unemitted node in the stack, pop that and emit that node's value and repeat step 3 with that right node
6. If no more unemitted nodes remain, stop

The common pattern is to implement a .iter method that will return a struct that implements std::iter::Iterator and emits references to the underlying tree. Before working on the code, we need to define the struct to hold the iterator state that holds the previously traversed nodes and the current tree:

#[derive(Debug)]
struct AvlTreeSetIter<'a, T: Ord> {
    prev_nodes: Vec<&'a AvlNode<T>>,
    current_tree: &'a AvlTree<T>,
}

impl<'a, T: 'a + Ord> Iterator for AvlTreeSetIter<'a, T> {
    type Item = &'a T;

    fn next(&mut self) -> Option<Self::Item> {
        unimplemented!()
    }
}

// Addition of lifetime parameter for the set
impl<'a, T: 'a + Ord> AvlTreeSet<T> {
    fn iter(&'a self) -> AvlTreeSetIter<'a, T> {
        AvlTreeSetIter {
            prev_nodes: Vec::new(),
            current_tree: &self.root,
        }
    }
}

Aside from treating std::vec::Vec as a stack, we need to discuss lifetime for parameters. This is one of Rust concepts that is conceptually easy but understanding the syntax requires practice. Fundamentally, every reference has a lifetime scope before being dropped that must not outlive the owner to avoid dangling references. Our iterator will not mutate or acquire ownership of the tree, instead it needs a reference to traverse it and that the iterator lives as long as the set itself. We express this by introducing a lifetime parameter('a) on each struct that is connected through the .iter. We also specify that emitted reference values also live as long as the iterator itself through the associated type (Item). Even with all this extra typing for lifetimes, the compiler is quite helpful in ensuring that the iterator safely references the set.

Another interesting discipline of Rust in thinking about the lifetime requirements of references as part of the design. My personal learning experience is to add explicit annotation for each reference, figure out their scope and then remove it if unnecessary as with lifetime elision. As much as possible, I let the Rust compiler infer as much and stepping in when needed.

Going back, when implementing Iterator::next method, we return Some(value) when we want to emit value and return None if we have no more. With this in mind, we can proceed:

fn next(&mut self) -> Option<Self::Item> {
    loop {
        match *self.current_tree {
            None => match self.prev_nodes.pop() {
                None => {
                    return None;
                }

                Some(ref prev_node) => {
                    self.current_tree = &prev_node.right;

                    return Some(&prev_node.value);
                }
            },

            Some(ref current_node) => {
                if current_node.left.is_some() {
                    self.prev_nodes.push(&current_node);
                    self.current_tree = &current_node.left;

                    continue;
                }

                if current_node.right.is_some() {
                    self.current_tree = &current_node.right;

                    return Some(&current_node.value);
                }

                self.current_tree = &None;

                return Some(&current_node.value);
            }
        }
    }
}

Although a bit longer, it just requires a little work. One thing I find interesting here is that pattern matching also has move semantics via ref keyword. Quite intriguing where borrow mechanics pervade even the familiar pattern matching. To show our code works, we insert a range backwards (Iterator::rev) and expect it to come up in ascending order:

let mut set = AvlTreeSet::new();

for i in (1..4 as usize).rev() {
    set.insert(i);
}

let mut iter = set.iter();
assert_eq!(iter.next(), Some(&1));
assert_eq!(iter.next(), Some(&2));
assert_eq!(iter.next(), Some(&3));
assert_eq!(iter.next(), None);

Can we test .iter without .insert? If we create a different constructor for our set that takes a collection or iterator and build nodes around it, we certainly could; however, it requires that we arrange them in a balanced manner which is beyond our current capacity. Testing both .iter and .insert is the simplest way to go.

Testing Insert

To test .iter and .insert together, we do the following:

1. Create a random list
2. Create an empty AVL tree and BTree
3. For each element in the list, insert it to both tree
4. Both AVL and BTree iterator should be equal item per item

For generating random data, we will use quickcheck as a generator and our testing style: property based testing. Instead of testing just correct input and output like with TDD and BDD, we focus on proving properties or statements are correct for every possible value. For example with odd and even integers, adding two even or odd integers will always be even while adding an even and odd integer together will always be odd. For testing abstract data types with little or no state, testing structural properties is easier than asserting the structure itself.

Our first statement/property is that our AVL tree and BTree have equal iterators since it exercises the whole structure and order. To assist in testing, we employ rust-itertools to test iterator equality via itertools::equal since it is better than using Iterator::zip and assert_eq! in a for loop. We also implement the convenience trait, std::iter::IntoIterator, to use IntoIterator::collect method to easily transforms iterators into other collections as shown below:

impl<T: Ord> FromIterator<T> for AvlTreeSet<T> {
    fn from_iter<I: IntoIterator<Item = T>>(iter: I) -> Self {
        let mut set = Self::new();

        for i in iter {
            set.insert(i);
        }

        set
    }
}

// The power of IntoIterator
let vec = (1..10 as u8).collect::<Vec<_>>();
let avl  = (1..10 as u8).collect::<AvlTreeSet<_>>();
let btree = (1..10 as u8).collect::<BTreeSet<_>>();

With all this foundation, creating a test for the iterator is precise:

#[cfg(test)]
mod properties {
    use super::*;
    use std::collections::BTreeSet;

    #[quickcheck]
    // 1. Create a random list
    fn iterator_parity(mut xs: Vec<usize>) -> bool {
        // 2. Create an empty AVL tree and BTree
        // 3. For each element in the list, insert it to both tree
        let avl_set = xs.iter().cloned().collect::<AvlTreeSet<_>>();
        let btree_set = xs.iter().cloned().collect::<BTreeSet<_>>();

        // 4. Both AVL and BTree iterator should be equal item per item
        equal(avl_set.iter(), btree_set.iter())
    }
}

Instead of #[test], we use #[quickcheck] macro to indicate it is a property based test. The actual mechanics of this style is that it will generate a random value each argument in the function, run the test and repeat it around 10,000 in an attempt to find a value that returns false or breaks the test. In this case, the test creates random usize lists and check the iterators as described above. The generated lists are also not sorted and not unique that challenges order and uniqueness. Until a counterexample is found, we can assume it correct.

We also check insert parity for completion:

#[quickcheck]
 fn insert_parity(mut btree_set: BTreeSet<u8>, x: u8) -> bool {
     let mut avl_set = btree_set.iter().cloned().collect::<AvlTreeSet<_>>();

     avl_set.insert(x) == btree_set.insert(x)
 }

Given an equal AVL and BTree set, .insert should be the same for every value. We can let quickcheck generate a random BTreeSet as well and copy it in the same manner. Since x is also random, it is either in the created sets or not that creates a positive and negative case for inserting duplicates. With both tests written, we run the tests with cargo test:

  Compiling avl_tree_set_rs v0.1.0 (/home/nobody/avl_tree_set_rs)
    Finished dev [unoptimized + debuginfo] target(s) in 0.91s
     Running target/debug/deps/avl_tree_set_rs-5f93a12c976aa84b

running 2 tests
test set::properties::iterator_parity ... ok
test set::properties::insert_parity ... ok

We now have a working tree set. Of course, since we did not rebalance the tree, we only crafted a standard binary tree but it is a start.

Reflection

Working with Rust in this first section is not bad. Going back to a static type system is reinvigorating. I really liked that structs, pattern matching and type classes were included in the language, so I had no problem there. Typing and understanding lifetime annotations is one thing that made Rust different. Understanding the wide array of traits and types itself is not trivial, so it is challenging how their lifetime are factored in as well.

As a beginner, taking some time to look at the various traits and types and their implementation made it click for me. Having the documentation at the ready with rustup doc --std was great tooling. Thankfully, we only require the basic concepts so it is more a learning experience. So far, Rust does play like a low-level modern language with some of the best modern features I value.

Rebalancing

With a working binary tree, we apply the rebalancing strategy by deciding how to implement height and node rotation. We then integrate it back to .insert and update our test.

• Balance Factor And Height
• Unsafe Decision
• Height Testing
• Node Rotation
• Rotation Testing
• Rebalancing Insert

Balance Factor And Height

Given a node, it has a balance factor that is the height of the left tree minus the height of the right tree. The idea is that when the balance factor grows to 2 or -2, a rotation of nodes or transfer of nodes from one side to the other will fix the balance. Starting with this definition, implementing the balance factor for nodes is direct with some type truncation safety:

impl<'a, T: 'a + Ord> AvlNode<T> {
    fn left_height(&self) -> usize {
        self.left.as_ref().map_or(0, |left| left.height())
    }

    fn right_height(&self) -> usize {
        self.right.as_ref().map_or(0, |right| right.height())
    }

    pub fn balance_factor(&self) -> i8 {
        let left_height = self.left_height();
        let right_height = self.right_height();

        if left_height >= right_height {
            (left_height - right_height) as i8
        } else {
            -((right_height - left_height) as i8)
        }
    }
}

Since our type uses usize, we need to consider subtraction overflow. Assuming the tree is balanced, the balance factor can only be from -2 to 2, so we can also use improve the return type from isize to i8 as a tiny optimization. However, if our tree does not update height properly, we will have overflow from the smaller datatype as a consequence. For the pragmatic, directly subtracting the left and right height and using isize is valid but still holds as a gentle reminder of what unsigned integers are and its design impact.

Anyway, we need to define a height field that is defined recursively as the larger height of the left or right subtree plus one and empty trees have an empty height of zero. Word-for-word, it is written as:

use std::cmp::max;

fn height(&self) -> usize {
    1 + max(
        self.left.as_ref().map_or(0, |node| node.height()),
        self.right.as_ref().map_or(0, |node| node.height()),
    )
}

Use Option::map_or when you need map and unwrap with a default in one go. However, updating ancestor nodes is expensive or inefficient when it traverses the same node multiple times, so we turn this into a field to cache the computation instead. Updating our definition of node:

struct AvlNode<T: Ord> {
    value: T,
    left: AvlTree<T>,
    right: AvlTree<T>,

    // New field
    height: usize,
}

impl<'a, T: 'a + Ord> AvlNode<T> {
    fn update_height(&mut self) {
        self.height = 1 + max(self.left_height(), self.right_height());
    }
}

After inserting or deleting a node, we need to traverse the ancestor nodes to update their height as a trade-off. Definitions done, implementing rotations was my first real struggle in Rust.

Unsafe Decision

How do we traverse upwards in our tree after every node insertion? A quick solution is to add a mutable reference to the parent node and use that to traverse until the root like so:

#[derive(Debug, PartialEq)]
struct AvlNode<'a, T: Ord> {
    value: T,
    left: AvlTree<'a, T>,    // Sad, extra annotations required
    right: AvlTree<'a, T>,
    height: usize,

    // New field
    parent_node: Option<&'a mut AvlNode<'a, T>>,
}

impl<'a, T: 'a + Ord> AvlNode<'a, T> {
    fn update_ancestors_height(&mut self) {
        self.update_height();

        let mut current_node = self;
        while let Some(parent_node) = current_node.parent_node {
            parent_node.update_height();
            current_node = parent_node;
        }
    }
}

However, this creates a cyclic reference between parent and child which is dangerous and discouraged in Rust. Personally, it also makes the design dirtier that requiring a reference only for traversing upwards on insert and delete operations seems overkill. Going back to .insert, we can track them with a stack instead via Vec::push mechanics:

fn insert(&mut self, value: T) -> bool {
    let mut prev_nodes = Vec::<&mut AvlNode<T>>::new();

    while let Some(current_node) = current_tree {
        prev_nodes.push(current_node);

        // match ...
    }

    // snip

    // Traversing a list as a stack needs to be reversed via .rev first
    for node in prev_nodes.into_iter().rev() {
        node.update_height();
    }

    true
}

The problem here is that current_node is mutable borrowed twice: one for a mutable left or right child node and one for traversed stack/vector. I would argue that the mutability of the tracking nodes is safe since it is used after the insert mutation is done. Crawling the web for idiomatic solutions, the suggested strategy is to use the combination of a reference counted pointer and interior mutable cell or Rc<RefCell<T>> pattern to allow multiple mutable references. I initially thought I could use this just in the function itself without changing the definition of the node but I could not:

use std::rc::Rc;
use std::cell::RefCell;

type AvlTree<T> = Option<Rc<RefCell<AvlNode<T>>>>;

To use them as intended, we would need to own the data we are using; however that is not possible since we are behind a mutable reference, &mut self. Even if I could make the code work, the fact that I had to change the types and include reference counting complicates the design needlessly just to retrace the nodes. Up to this point, I find Rust's strictness comforting in spite of my struggle; however, I feel that I need to loosen up the restriction a bit to avoid unnecessary complexity. In this case, we want to allow one secondary mutable reference after insertion and doing this requires Unsafe Rust. Unsafe Rust allows us to ignore borrowing rules for mutability as specified in this section of the book. Using raw pointers allows our implementation to be uncomplicated:

fn insert(&mut self, value: T) -> bool {
    let mut prev_ptrs = Vec::<*mut AvlNode<T>>::new();

    while let Some(current_node) = current_tree {
        prev_ptrs.push(&mut **current_node);   // Converting a mutable reference to a pointer

        // ... match ...
    }

    // ... insert ...

    for node_ptr in prev_ptrs.into_iter().rev() {
        let node = unsafe { &mut *node_ptr };  // Converting a mutable pointer back to a reference
        node.update_height();
    }

    true
}

The arcane magic of unsafe is better explained in the Rustonomicon which I plan to read after writing this. Since we told Rust to trust us, we need to guarantee our function is safe. The most visible angle is the one using unsafe or the raw pointers themselves. The mutable method, .update_height, only requires that its children have the correct height before updating itself. As an anecdote, I forgot to reverse the list before iterating (since push operation append at the end) and caused incorrect node heights because the parents were updated before the children. With this possibility, we also need to test the height property.

Height Testing

Given any AVL tree set, each node's height is one more than the larger height of the left or right subtree. To make testing easier, we can do two short things. First, instead of pattern matching the structure, we can refactor .iter to emit the nodes instead of their values .node_iter:

impl<'a, T: 'a + Ord> AvlTreeSet<T> {
    // Using impl Traits
    fn iter(&'a self) -> impl Iterator<Item = &'a T> + 'a {
        self.node_iter().map(|node| &node.value)
    }

    fn node_iter(&'a self) -> impl Iterator<Item = &'a AvlNode<T>> + 'a {
        AvlTreeSetNodeIter {
            prev_nodes: Vec::default(),
            current_tree: &self.root,
        }
    }
}

As an aside, I suggest learning impl Traits that allows you to return an abstract trait type instead of the concrete type as in polymorphism. Using that, we can implement generic iterator adapters for .iter that maps over .node_iter. Without it, creating abstractions on top of another becomes a noisy type fest:

use core::iter::Map;

fn iter(&'a self) -> Map<AvlTreeSetNodeIter<'a, T>, fn(&'a AvlNode<T>) -> &T> {
    self.node_iter().map(|node| &node.value)
}

fn node_iter(&'a self) -> AvlTreeSetNodeIter<'a, T> {
    AvlTreeSetNodeIter {
        prev_nodes: Vec::default(),
        current_tree: &self.root,
    }
}

Going back, the new AvlTreeSetNodeIter is a copied version of the original iterator with Some(&current_node.value) replaced to Some(&current_node). Moving on the second item, instead of creating the sets through .collect method; we can also have it generated by implementing the Arbitrary trait ourselves:

use quickcheck::{Arbitrary, Gen};

// Refit and copied from quickcheck
// https://docs.rs/quickcheck/0.8.5/src/quickcheck/arbitrary.rs.html#385-395
impl<T: Arbitrary + Ord> Arbitrary for AvlTreeSet<T> {
    fn arbitrary<G: Gen>(g: &mut G) -> Self {
        let vec: Vec<T> = Arbitrary::arbitrary(g);
        vec.into_iter().collect()
    }

    fn shrink(&self) -> Box<dyn Iterator<Item = Self>> {
        let vec: Vec<T> = self.iter().cloned().collect();
        Box::new(vec.shrink().map(|v| v.into_iter().collect::<Self>()))
    }
}

Putting those two together, we have another simple test:

use std::cmp::max;
use itertools::all;

#[quickcheck]
fn node_height(set: AvlTreeSet<u16>) -> bool {
    all(set.node_iter(), |node| {
        node.height == 1 + max(node.left_height(), node.right_height())
    })
}

Another succinct test that .update_height correctly updates the child all the way up to the root and that our use of unsafe is truly safe. Whether you agree with my use of unsafe, I learned a certain reverence in asking permission to use dangerous features and heightened responsibility in upholding the law that reminds me of Haskell's IO boundaries. Nonetheless, we can now tackle node rotation.

Node Rotation

After inserting a node in a balanced AVL tree, it becomes imbalanced when a node has a left and right subtree height difference of 2 or -2. To correct this, we move nodes around while preserving order. Visualizing the operation for rotating nodes to the right:

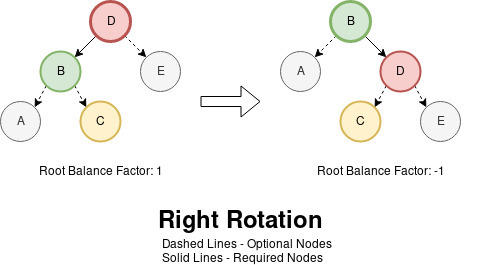
Given a node, the idea is to promote the left child as the root and demote the old root as a right child. While retaining other node relationships, the orphaned left-right child of the old root is now the right-left child of the new root. Those two movements constitute the right rotation of nodes. As a general observation, moving nodes from one side to the other should change the balance factor. Based on the diagram above, we can say it changes by 2 perhaps. We'll verify this observation later.

Implementing the rotation took me a long time to do with two primary constraints. First was to avoid using unsafe again. Another is to avoid create another node or heap allocated pointer via Box::new to be memory efficient. After several attempts, I came up with this safe implementation of right rotation:

use std::mem::{replace, swap};

impl<'a, T: 'a + Ord> AvlNode<T> {
    fn rotate_right(&mut self) -> bool {
        if self.left.is_none() {
            return false;
        }

        // 1. Take nodes A and C
        let left_node = self.left.as_mut().unwrap();
        let left_right_tree = left_node.right.take();
        let left_left_tree = left_node.left.take();

        // 2. Link A node to left node
        let mut new_right_tree = replace(&mut self.left, left_left_tree);
        // 3. Swap B and D node value to avoid moving the root
        swap(&mut self.value, &mut new_right_tree.as_mut().unwrap().value);
        // 4. Take E node
        let right_tree = self.right.take();

        // 5. Link C and E nodes to swapped D node
        let new_right_node = new_right_tree.as_mut().unwrap();
        new_right_node.left = left_right_tree;
        new_right_node.right = right_tree;
        // 6. Link swapped D node to root right node
        self.right = new_right_tree;

        if let Some(node) = self.right.as_mut() {
            node.update_height();
        }

        self.update_height();

        true
    }
}

By carefully using std::mem::swap and std::mem::replace, we avoid creating nodes by replacing the value and links of an existing node instead. The main idea is about taking nodes from the left side and placing them on the right carefully. Referring to the rotation diagram while stepping through the code might help. After rotating, we also need to update the heights of the right tree and the node itself since they had new nodes. One minor thing is that we also return a flag to indicate that the operation was executed or not for our tests later. To compare and contrast, my first version is indeed shorter yet memory inefficient:

pub fn rotate_right(&mut self) -> bool {
    // snip

    let left_right_tree = self.left.as_mut().unwrap().right.take();
    let new_root = *replace(&mut self.left, left_right_tree).unwrap();
    let old_root = replace(self, new_root);

    replace(&mut self.right, Some(Box::new(old_root))); // New pointer created here

    // snip
}

Assuming it is correct in either version, implementing the left rotation is a bit of cheat by swapping every left with right text in the function since they are symmetrical. To say that we have working and safe rotations after days of working back and forth is nothing short of bliss. As we did before, we need to prove it works.

Rotation Testing

We have two statements to test about node rotation: rotations should preserve order and adjust the balance factor. With everything previously setup, we can test the first statement directly:

use quickcheck::TestResult;

#[quickcheck]
fn rotate_right_preserves_order(btree: BTreeSet<u8>) -> TestResult {
    let mut set = btree.iter().cloned().collect::<AvlTreeSet<_>>();

    if !set.root.is_some() {
        return TestResult::discard();
    }

    if !set.root.as_mut().unwrap().rotate_right() {
        return TestResult::discard();
    }

    TestResult::from_bool(equal(set.iter(), btree.iter()))
}

Given a BTree, we clone that to an AVL and right rotate the root node and check if the resulting iterators still matches in order and value. We also want to ignore empty trees and nodes that cannot not be rotated since they do not add value. For that, we use the discard test mechanics of quickcheck with a quickcheck::TestResult output instead. If a test is discarded, a new test sample is created instead of ignoring it that would have eaten the maximum number of tests. Same tactic applies to writing the left rotation.

First statement down, we now check if right rotation does tilt the balance factor say by 2:

#[quickcheck]
fn rotate_right_tils_balance_factor(xs: Vec<u32>) -> TestResult {
    let mut set = xs.iter().cloned().collect::<AvlTreeSet<_>>();

    if !set.root.is_some() {
        return TestResult::discard();
    }

    let root_node = set.root.as_mut().unwrap();
    let balance_factor = root_node.balance_factor();

    if !root_node.rotate_right() {
        return TestResult::discard();
    }

    let tilted_factor = root_node.balance_factor();

    TestResult::from_bool(balance_factor - tilted_factor == 2)
}

Running just this test with cargo test rotate_right_tilts_balance_factor, this test fails on the list [2, 0, 1]:

    Finished dev [unoptimized + debuginfo] target(s) in 0.01s
     Running target/debug/deps/avl_tree_set-ac5259255f5174fd

running 1 test
thread 'set::properties::rotate_right_tilts_balance_factor' panicked at '[quickcheck] TEST FAILED. Arguments: ([2, 0, 1])',
/* More errors */

Visualizing this counterexample:

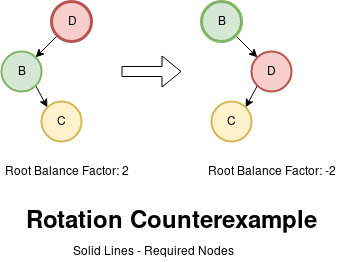
Given this diagram, the balance factor is changed from 2 to -2 that has a difference of 4 that fails the test. Even accommodating that, the next counterexample is [2, 0, 1, 3] where the balance factor is 1 turned to -2 with a difference of 3. With subsequent exploration, the difference is always at least 2 but the upper bound is unknown. This is where property based testing is meaningful in expanding our empirical observation. Nonetheless, the tilt still exists that proves that the rotation works although weakly. We then update the condition to test a difference of at least 2 to pass and apply a similar treatment to writing the left rotation test.

To connect these two rotations in one property, what can we say about those two operations when applied together? Can we say they are inverse operations that a right rotation undoes a left rotation or vice-versa like with multiplication and division? Again, easily verified:

#[quickcheck]
fn rotate_left_and_rotate_left_identity(set: AvlTreeSet<u8>) -> TestResult {
    if set.root.is_none() {
        return TestResult::discard();
    }

    let mut rotated_set = set.clone();
    let root_node = rotated_set.root.as_mut().unwrap();

    if root_node.rotate_left() {
        root_node.rotate_right();
    } else {
        root_node.rotate_right();
        root_node.rotate_left();
    }

    TestResult::from_bool(rotated_set == set)
}

Given a set, we clone that and rotate left then right or whichever applies first, then check if it is the same structure. Running the test proves it is valid since no breaking example can be found:

   Compiling avl_tree_set v0.1.0 (/home/nobody/avl_tree_set_rs)
    Finished dev [unoptimized + debuginfo] target(s) in 0.27s
     Running target/debug/deps/avl_tree_set-ac5259255f5174fd

running 5 tests
test set::properties::rotate_left_and_rotate_left_identity ... ok
test set::properties::rotate_left_tilts_balance_factor ... ok
test set::properties::rotate_right_tilts_balance_factor ... ok
test set::properties::rotate_left_preserves_order ... ok
test set::properties::rotate_right_preserves_order ... ok
/* Omitted other results */

With confidence from those supporting statements, we are now ready to finish our insert method.

Rebalancing Insert

If we have an imbalanced node, then wouldn't one correct rotation restore balance? It is a good first intuition but our small counterexample on the tilt property disproves that. However, we can apply another rotation to a child node before applying the main rotation and it is enough to work. You can find a mathematical proof of induction here if you are interested. Theory aside, the algorithm can be thought of as branching paths:

1. Give a root node, if the balance factor is 2 (left heavy), we inspect the left node.
2. If the left node has a balance factor of 1 (left heavy), we just right rotate on the root node.
3. Otherwise, we left rotate this inner left node and right rotate the root node.
4. Going back to the root node, if the balance factor is instead -2 (right heavy), we inspect the right node.
5. If the right node has a balance factor of -1 (right heavy), we just left rotate the root node.
6. Otherwise, we right rotate the inner right node and left rotate the root node.

Translating this into code is rather direct with pattern matching:

impl<'a, T: 'a + Ord> AvlNode<T> {
    fn rebalance(&mut self) -> bool {
        match self.balance_factor() {
            -2 => {
                // Root is right heavy
                let right_node = self.right.as_mut().unwrap();

                // Inner node is left heavy
                if right_node.balance_factor() == 1 {
                    right_node.rotate_right();
                }

                self.rotate_left();

                true
            }

            2 => {
                // Root is left heavy
                let left_node = self.left.as_mut().unwrap();

                // Inner node is right heavy
                if left_node.balance_factor() == -1 {
                    left_node.rotate_left();
                }

                self.rotate_right();

                true
            }
            _ => false,
        }
    }
}

We directly integrate this method back to .insert as planned:

fn insert(&mut self, value: T) -> bool {
    // snip

    for node_ptr in prev_ptrs.into_iter().rev() {
        let node = unsafe { &mut *node_ptr };

        node.update_height();
        node.rebalance();    // Right here
    }

    true
}

To test the rebalancing property, we assert that every node should not be imbalanced which is similar to the height test:

#[quickcheck]
fn balanced_nodes(set: AvlTreeSet<u16>) -> bool {
    all(set.node_iter(), |node| node.balance_factor().abs() < 2)
}

Running this and all prior test specially with the height and iterator property proves that our tree is balanced after every insert:

   Compiling avl_tree_set v0.1.0 (/home/nobody/avl_tree_set_rs)
    Finished dev [unoptimized + debuginfo] target(s) in 0.27s
     Running target/debug/deps/avl_tree_set-ac5259255f5174fd

running 3 tests
test set::properties::balanced_nodes ... ok
test set::properties::node_height ... ok
test set::properties::iterator_parity ... ok
/* Omitting other tests */

We now have a self-balancing tree and can now proclaim victory.

Reflection

This was a challenging section. In particular with rotation, it was hard to negotiate with the compiler how to move the nodes correctly. In my darkest hour, I was truly tempted to use unsafe to move the pointers directly (if I could) as C code seems so deceptively easy; however, I would increase the error margin/surface of the design. This problem was less about writing and technicalities but more about understanding that requires patience and rigor. After this, I stopped resisting the compiler and started to accept it.

Deletion

After all the struggle with .insert, the deletion method, .take, is surprisingly the harder of the two methods. When deleting nodes, we have to handle three cases for the deleted node to maintain the tree structure: no children, one child and two children. This section is a culmination of all the techniques.

• Delete Method
• Zero Or One Child
• Two Children
• Deletion Testing

Delete Method

Parity: BTreeSet::take

If you noticed Option::take when rotating nodes, it returns the owned value and internally replaced by a None value. For our tree, our .take method follows the same convention. Here is the whole procedure to delete a node:

1. Starting from the root node or with a current node
2. Move to the left node if the value is less than the current node, right if greater
3. Do this until you have a node equal to that value, otherwise stop
4. Delete that node and return the value
5. If the deleted node has no children, stop
6. If the deleted node has one child, substitute that child to the removed node
7. If the deleted node has two children, substitute the deleted node with the leftmost child of the right subtree and link the orphaned left child to the left child of this new node

These steps are short to write but are deceptively tricky but the first few are done in the same manner as we did with .insert:

fn take(&mut self, value: &T) -> Option<T> {
    let mut prev_ptrs = Vec::<*mut AvlNode<T>>::new();
    // 1. Starting from the root node or with a current node
    let mut current_tree = &mut self.root;
    let mut target_value = None;

    while let Some(current_node) = current_tree {
        // 2. Move to the left node if the value is less than the current node,
        //    right if greater
        match current_node.value.cmp(&value) {
            Ordering::Less => {
                prev_ptrs.push(&mut **current_node);
                current_tree = &mut current_node.right;
            }
            Ordering::Equal => {
                // 3a. Do this until you have a node equal to that value, ...
                target_value = Some(&mut **current_node);
                break;
            }
            Ordering::Greater => {
                prev_ptrs.push(&mut **current_node);
                current_tree = &mut current_node.left;
            }
        };
    }

    // 3b. ... otherwise stop
    if target_value.as_ref().is_none() {
        return None;
    }

    let target_node = target_value.unwrap();

    // 4. Delete that node and return the value
    let mut taken_value = ???;

    // Retrace the path and update them accordingly
    for node_ptr in prev_ptrs.into_iter().rev() {
        let node = unsafe { &mut *node_ptr };
        node.update_height();
        node.rebalance();
    }

    Some(taken_value)
}

This is the .insert method with some modifications. We need the node before .insert stops, so the target_value captures that idea. It is also wrapped in an Option to see check if a node is found and stop otherwise. Also, we use taken_value as the return value after deleting the node. Before exiting, we make sure the tracked nodes are updated before we leave.

To emphasize, deleting or relocating nodes is a tricky operation since it potentially moves many nodes. We exercise care as we handle each case and consider height and balance if needed. Failing to update nodes correctly will lead to subtle memory issues such as mentioned in .balance_factor and dropped nodes. We naturally start with the safer case of zero or one child for the deleted node.

Zero Or One Child

The case of deleting an empty node is about detaching the target node. With one child either left or right, we still delete the node and promote that child in its place. Weirdly, the case of deleting one child is easier than deleting no child:

fn take(&mut self, value: &T) -> Option<T> {
    // snip

    // Deleting the node here
    let taken_value = if target_node.left.is_none() || target_node.right.is_none() {
        if let Some(left_node) = target_node.left.take() {
            replace(target_node, *left_node).value
        } else if let Some(right_node) = target_node.right.take() {
            replace(target_node, *right_node).value
        } else {
            // Deleting an no children
        }
    } else {
        unimplemented!()
    }

    // snip
}

The tactic of the deleting node with replace allows us to get ownership of the node that gives us ownership of the value we want to return. Since a child tree was promoted, no height or rebalancing is needed for the replaced node.

With the one child node, we can get a node and replace the deleted node with that. With no children, we cannot use the same tactic. Instead, we have to go the parent node and delete if from there:

if let Some(left_node) = target_node.left.take() {
    // snip
} else if let Some(right_node) = target_node.right.take() {
    // snip
} else {
    // 1a. Get parent node
    if let Some(prev_ptr) = prev_ptrs.pop() {
        let prev_node = unsafe { &mut *prev_ptr };

        // 1b. Determine which node to remove: left or right node
        let inner_value = if let Some(ref left_node) = prev_node.left {
            if left_node.value == target_node.value {
                prev_node.left.take().unwrap().value
            } else {
                prev_node.right.take().unwrap().value
            }
        } else {
            prev_node.right.take().unwrap().value
        };

        // 2. Update parent node
        prev_node.update_height();
        prev_node.rebalance();

        // 3. Return value
        inner_value
    } else {
        // 1c. ... otherwise it is the parent and take the root node
        self.root.take().unwrap().value
    }
}

Given the parent node, we determine which left or right node to take by checking for equality once again. We could create an extra enum or flag to remember the path, but it is a minor trade-off than adding state. Either way, we take that node and returns its value; however, since the parent node had a child removed, we update it accordingly. Lastly, it is possible no previous nodes were traversed that implies it is an isolated root node to delete which is easily handled. Another case where pattern matching helps with illuminating edge cases. With some confidence in our reasoning, we handle the hard case of two children.

Two Children

For two children, we replace the deleted node with the node of the next value or the leftmost child of the right child of the deleted node:

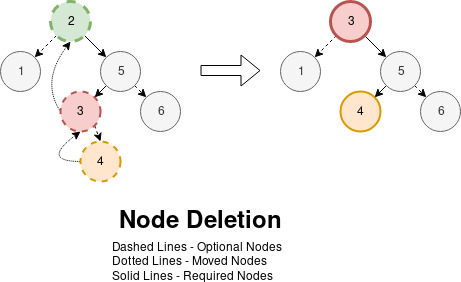
Describing the algorithm:

1. Starting with the right child of the target node
2. Keep moving the current node to the left child until it has none
3. Replace the target node value with the current node value
4. Replace the current node with the right child if it has one

Applying all the prior techniques for this final challenge:

let taken_value = if target_node.left.is_none() || target_node.right.is_none() {
    // snip
} else {
    let right_tree = &mut target_node.right;

    // 1. Starting with the right child of the target node
    let mut next_tree = right_tree;
    // We also keep track of the parent nodes to update the height
    let mut inner_ptrs = Vec::<*mut AvlNode<T>>::new();

    // 2. Keep moving the current node to the left child until it has none
    while let Some(next_left_node) = next_tree {
        if next_left_node.left.is_some() {
            inner_ptrs.push(&mut **next_left_node);
        }
        next_tree = &mut next_left_node.left;
    }

    // We don't use next_tree but instead the tracked nodes as basis
    let parent_left_node = unsafe { &mut *inner_ptrs.pop().unwrap() };
    let mut leftmost_node = parent_left_node.left.take().unwrap();

    // 3. Replace the target node value with the current node value
    let inner_value = replace(&mut target_node.value, leftmost_node.value);
    // 4. Replace the current node with the right child if it has
    replace(&mut parent_left_node.left, leftmost_node.right.take());

    // Updates the nodes in order
    parent_left_node.update_height();
    parent_left_node.rebalance();

    for node_ptr in inner_ptrs.into_iter().rev() {
        let node = unsafe { &mut *node_ptr };
        node.update_height();
        node.rebalance();
    }

    target_node.update_height();
    target_node.rebalance();

    inner_value
}

It is quite a mouthful and the last bit of complex code. It is like an inner delete based on the child right tree that follows the same conventions. After promoting a bottom node, we have an interesting path of nodes to update and balance: the parent of the leftmost child up to the originating target node. Stepping through the code should be straightforward although more complex.

For the astute reader, we have one final edge case as the code above assumes that at least one tracked node always exist by the declaration of parent_left_node that only happens when the direct right node has no left child based on the diagram. In that simpler yet similar case, we replace that node with the right child if has any:

let right_tree = &mut target_node.right;

if right_tree.as_ref().unwrap().left.is_none() {
    let mut right_node = right_tree.take().unwrap();

    let inner_value = replace(&mut target_node.value, right_node.value);
    replace(&mut target_node.right, right_node.right.take());

    target_node.update_height();
    target_node.rebalance();

    inner_value
} else {
    // Previous case
}

With that final edge case, the .take method is complete and ready to test.

Deletion Testing

To test deletion, we need to test for existence that we do by finally implementing a BTreeSet::contains method. With everything done so far, this is a relief:

impl<'a, T: 'a + Ord> AvlTreeSet<T> {
    pub fn contains(&self, value: &T) -> bool {
        let mut current_tree = &self.root;

        while let Some(current_node) = current_tree {
            match current_node.value.cmp(&value) {
                Ordering::Less => {
                    current_tree = &current_node.right;
                }
                Ordering::Equal => {
                    return true;
                }
                Ordering::Greater => {
                    current_tree = &current_node.left;
                }
            };
        }

        false
    }
}

Given an equal AVL and BTree set, .contains should be the same for every value. Testing .contains will have a little twist. We want to have a more defined positive and negative test cases, so when cloning a list of numbers, we only include the even numbers as positive cases and odd as negatives:

#[quickcheck]
fn contains_parity(xs: Vec<isize>) -> bool {
    let evens = xs
        .iter()
        .cloned()
        .filter(|x| x % 2 == 0)
        .collect::<Vec<_>>();

    let avl_set = evens.iter().cloned().collect::<AvlTreeSet<_>>();
    let btree_set = evens.iter().cloned().collect::<BTreeSet<_>>();

    all(xs.iter(), |x| avl_set.contains(x) == btree_set.contains(x))
}

As long as we have a subset of data, it is valid. Also we do not need to filter test cases so we revert back to the familiar test template. Assuming the test works, we use the same template of positive and negative testing for .take as well. Thanks to the previous sections, we establish our tree has three core properties:

1. Ordering
2. Height
3. Balanced

If we prove that each property holds after several deletions, it shows our tree is balanced and correct. Writing a separate test for each one might be more verbose, but it makes failing properties easier to reason about.

Given an equal AVL and BTree set, .take should be the same for every value. Before we check the core properties, we test if the interface is correct:

#[quickcheck]
fn take_parity(xs: Vec<usize>) -> bool {
    let odds = xs
        .iter()
        .cloned()
        .filter(|x| x % 2 == 1)
        .collect::<Vec<_>>();
    let mut avl_set = odds.iter().cloned().collect::<AvlTreeSet<_>>();
    let mut btree_set = odds.iter().cloned().collect::<BTreeSet<_>>();

    all(xs.iter(), |x| avl_set.take(x) == btree_set.take(x))
}

Establishing the methods are equal, we then test the first property which is our comfortable iterator equality test.

#[quickcheck]
fn take_iterator_parity(xs: Vec<i16>) -> bool {
    let fives = xs
        .iter()
        .cloned()
        .filter(|x| x % 5 == 0)
        .collect::<Vec<_>>();
    let mut avl_set = xs.iter().cloned().collect::<AvlTreeSet<_>>();
    let mut btree_set = xs.iter().cloned().collect::<BTreeSet<_>>();

    for five in fives {
        assert_eq!(avl_set.take(&five), btree_set.take(&five));
    }

    equal(avl_set.iter(), btree_set.iter())
}

Aside from order, this guarantees our deletion does delete the correct nodes and preserves the others. Next one is height via node iterator:

#[quickcheck]
fn take_height_nodes(xs: Vec<isize>) -> bool {
    let negatives = xs.iter().cloned().filter(|&x| x < 0).collect::<Vec<_>>();
    let mut set = xs.iter().cloned().collect::<AvlTreeSet<_>>();

    for negative in negatives {
        set.take(&negative);
    }

    all(set.node_iter(), |node| {
        node.height == 1 + max(node.left_height(), node.right_height())
    })
}

Having correct heights is a good sign that nodes are updated properly. Topping it off, the balance factor is checked with the same mechanics:

#[quickcheck]
fn take_balanced_nodes(xs: Vec<usize>) -> bool {
    let odds = xs
        .iter()
        .cloned()
        .filter(|x| x % 2 == 1)
        .collect::<Vec<_>>();n
    let mut set = xs.iter().cloned().collect::<AvlTreeSet<_>>();

    for odd in odds {
        set.take(&odd);
    }

    all(set.node_iter(), |node| node.balance_factor().abs() < 2)
}

Running the tests one last time proves victorious:

   Compiling avl_tree_set_rs v0.1.0 (/home/nobody/avl_tree_set_rs)
    Finished dev [unoptimized + debuginfo] target(s) in 0.12s
     Running target/debug/deps/avl_tree_set_rs-551042db094327bb

running 4 tests
/* Passing previous tests */
test set::properties::take_height_nodes ... ok
test set::properties::take_balanced_nodes ... ok
test set::properties::take_iterator_parity ... ok
test set::properties::take_parity ... ok

Reflection

Originally, I used rspec and fake-rs as my testing strategy that gave me a good quality test workflow. In writing this article, I moved to quickcheck as a better paradigm to test abstract data structure. Aside from being easier to write and iterate, porting my tests to this paradigm gave me failing tests specially on this dangerous method. That was a good catch that also gave me better and smaller counterexamples to find the memory issues in my code.

Aside from property based testing against a memory issue, working on deletion is not that technical or hard. The prior two sections have trained me to implement the algorithm with no fuzz. I am at peace, I am productive.

Beyond Parity

In this article, we are done with the major goals of our project. During my spare time, I implemented every struct method (not traits) from BTreeSet to AvlTreeSet as practice. While insertion and deletion were the hardest methods, everything else was cakewalk, so checkout the code repository if completion piques your interest. This optional section is about a few things I found interesting.

• Benchmark
• Memory Safety

Benchmark

As a minor fancy, how does our implementation perform against the standard library? Consulting a benchmarking chapter, we can benchmark the insert operation by generating random numbers and timing it using this shortened snippet:

#[bench]
fn setup_random_btree_set(b: &mut Bencher) {
    let mut rng = thread_rng();
    let mut set = BTreeSet::new();

    b.iter(|| {
        set.insert(rng.gen::<usize>());
    });
}

#[bench]
fn setup_random_avltree_set(b: &mut Bencher) {
    let mut rng = thread_rng();
    let mut set = AvlTreeSet::new();

    b.iter(|| {
        set.insert(rng.gen::<usize>());
    });
}

Here, we use rand crate to generate random numbers outside of quickcheck to populate our set and the base set. We conveniently have a builtin cargo bench command that works out of the box, so we can just run cargo bench and watch:

    Finished release [optimized] target(s) in 0.04s
     Running target/release/deps/avl_tree_set_rs-e74d4a8db1cacec9

running 17 tests
/* Passing prior tests */
test bench::setup_random_avltree_set ... bench:       1,800 ns/iter (+/- 517)
test bench::setup_random_btree_set   ... bench:         529 ns/iter (+/- 72)

In this run, our toy set has insert performance that is more or less four times slower than what Rust has matured. It would be strange if it was significantly close. As simple as .insert is, the bottleneck possibly lies in the rotations since they use many .take or memory operations which could be further optimized. We now have a general sense of relative performance for our implementation.

Memory Safety

Aside from the promise of safety, can we further prove our library has no memory leaks? Asking this question lead me to this article and valgrind: a memory error detector. Installing it and creating a small main bin.rs file that generates a set and removes every element:

use avl_tree_set::set::AvlTreeSet;

pub fn main() {
    let mut set = (1..10_000 as u32).rev().collect::<AvlTreeSet<_>>();

    for i in 1..10_000 {
        set.take(&i);
    }
}

Compiling it into an executable via cargo build and running valgrind --leak-check=full ./target/debug/avl_tree_set

==25728== Memcheck, a memory error detector
==25728== Copyright (C) 2002-2017, and GNU GPL'd, by Julian Seward et al.
==25728== Using Valgrind-3.16.0.GIT and LibVEX; rerun with -h for copyright info
==25728== Command: ./target/debug/avl_tree_set
==25728==
==25728==
==25728== HEAP SUMMARY:
==25728==     in use at exit: 0 bytes in 0 blocks
==25728==   total heap usage: 101,389 allocs, 101,389 frees, 4,198,985 bytes allocated
==25728==
==25728== All heap blocks were freed -- no leaks are possible
==25728==
==25728== For lists of detected and suppressed errors, rerun with: -s
==25728== ERROR SUMMARY: 0 errors from 0 contexts (suppressed: 0 from 0)

Having an external tool check our small executable reveals no memory leaks that is comforting and assuring along with passing tests. With the code before I started writing this article, I followed the same steps above with passing tests, I ran into the following:

==3010== Memcheck, a memory error detector
==3010== Copyright (C) 2002-2017, and GNU GPL'd, by Julian Seward et al.
==3010== Using Valgrind-3.16.0.GIT and LibVEX; rerun with -h for copyright info
==3010== Command: ./target/debug/avl_tree_set
==3010==
==3010== Invalid read of size 8
==3010==    at 0x1104BE: core::option::Option<T>::as_ref (option.rs:239)
==3010==    by 0x10EF32: avl_tree_set::tree::AvlNode<T>::left_height (tree.rs:16)
==3010==    by 0x10F942: avl_tree_set::tree::AvlNode<T>::update_height (tree.rs:24)
==3010==    by 0x112ABA: avl_tree_set::set::AvlTreeSet<T>::take (set.rs:107)
==3010==    by 0x11113A: avl_tree_set::main (bin.rs:7)
==3010==    by 0x113E6F: std::rt::lang_start:: (rt.rs:64)
==3010==    by 0x11A9B2:  (rt.rs:49)
==3010==    by 0x11A9B2: std::panicking::try::do_call (panicking.rs:294)
==3010==    by 0x11C319: __rust_maybe_catch_panic (lib.rs:82)
/* More errors down below */

Conflicted with passing tests and a memory issue I could not replicate in test, my denial thought that valgrind was broken instead. Switching to property based test helped in finding test cases that causes memory issues. The offending code happens with the deletion of a leaf node in the old code:

if let Some(prev_ptr) = prev_ptrs.pop() {
    // snip

    prev_node.update_height();
    prev_node.rebalance();

    // Memory issue
    target_node.update_height();
    target_node.rebalance();

    inner_value
} else {
    self.root.take().unwrap().value
}

Recall in the no children case, we detach the target_node and updated the prev_node instead. I forgot about that assumption and carelessly updated the deleted node and remember that prev_node comes from an unsafe pointer that breaks the single mutable reference rule. Perhaps, target_node has a child that that was part of the rotation and became a dangling pointer afterwards. Although our use of unsafe was seemingly safe, my tests did not catch that. As proud as I was of my old tests, having external tools offer insights outside my ego and bias. So even when the code compiles and passes, it is good to check running code.

Reflecting On Rust

Although not a shining example of AVL Trees, it has been a good first project. I believe it was a good vertical slice of Rust. In the beginning, understanding, patience and perseverance is required with the new idioms and designs and specially for the compiler. Working through the code, familiarizing new functions and traits and grasping lifetimes were the only difficulty. Reflecting on its style, it is a happy union/mix between object oriented and functional. Overall, Rust is overall a challenging yet rewarding language with little to complain syntactically.

Looking back on Ruby and Elixir, I frequently find myself looking for the & or borrow operator in the variables. Working with the Borrow Checker, I believe, has been a positive experience although rigorous. As such, I realize that this intricate mechanism cannot easily be ported to other language without design considerations. If Elixir had Rust's mechanics, I doubt it would be as popular or as ergonomic in its (almost) actor/process model. (Perhaps Pony language will be the evolved version when it matures?) As a modern observation, languages that value a form application safety (memory, data, correctness) tends to have higher learning curves and barriers to entry because of the required mindset and philosophies. With better ergonomics, documentation and tooling, the learning curve is somewhat balanced. So despite its accessibility, Rust definitely deserves attention and discussion for its rare core value of safety.

This was a long article to prepare and write, so thank you for making it to the end. I hope you found the journey meaningful or valuable in some way. What is the next learning project? Aside from reading The Rustonomicon first, here are some project ideas:

Make a Lisp in Rust

Implementing a (LISP) language is a dream.

GraphQL Server

Is Rust good for the usual web development or microservices?

Web Scraping/Crawling

A good opportunity to learn asynchronous and concurrent operations.

C Interop

How good is the workflow in integrating with native libraries?

Web Assembly

A backend language in the browser is interesting

As a newcomer, I am excited with the new doors Rust has opened for me. For now, I feel ecstatic in writing a valid library that I am confidently safer than it would be in C. That is good enough for me.